Art‑Style Beam Reinforcement Calculator

—

—

An Ultimate Guide to Beam Reinforcement Calculation

Look at any building, bridge, or overpass. You see concrete—vast, solid, and seemingly indestructible. It’s the face of modern construction, a symbol of permanence and strength. But the true secret to its power is hidden from view, buried deep within. It’s an intricate skeleton of steel, a network of precisely placed bars known as reinforcement.

Without this hidden skeleton, a concrete beam spanning more than a few feet would be as fragile as a cracker, ready to snap under its own weight. It’s the silent, symbiotic partnership between brittle concrete and ductile steel that makes our modern world possible.

But how do engineers decide exactly how much steel to use? How do they know the perfect size, number, and placement of these bars to ensure a beam can support a floor, a roof, or a fleet of trucks for a hundred years without fail?

It’s not guesswork. It’s a fascinating and critical process of calculation, a blend of physics, material science, and meticulous adherence to safety codes.

Welcome to the ultimate guide to beam reinforcement calculation. This isn’t a dry textbook chapter. This is a deep dive for the curious mind—the civil engineering student, the junior engineer looking to sharpen their skills, the architect wanting to understand the structures they design, or the passionate DIYer who wants to peek behind the curtain of structural engineering.

We will start with the fundamental “why,” build a dictionary of essential terms, walk through the governing principles of design codes, and then—the main event—we will perform a complete, step-by-step flexural and shear design of a concrete beam from scratch.

Grab your calculator, and let’s uncover the secrets of this unseen strength.

Chapter 1: The Perfect Partnership: Why Concrete Needs Steel

Before a single number is crunched, you must understand why this process is necessary. The entire field of reinforced concrete design hinges on one simple fact: concrete and steel are a dream team with perfectly complementary superpowers.

Concrete: The Mighty but Brittle Giant

Concrete is, in a word, a rock. And like a rock, it has phenomenal compressive strength. You can squeeze it, stand on it, and stack immense weight on top of it, and it will barely flinch. This is why it’s the material of choice for columns and foundations.

However, concrete has a fatal flaw: it has abysmal tensile strength. If you try to pull it apart or bend it, it fails suddenly and catastrophically. Its tensile strength is often less than 10% of its compressive strength.

Imagine a simple, unreinforced concrete beam supported at both ends. When you push down on the middle, the beam bends. The top surface gets squeezed together (compression), which the concrete handles beautifully. But the bottom surface gets stretched apart (tension). The instant that tension becomes too much, a crack forms at the bottom and rips upward in a split second. The beam snaps.

Steel: The Flexible and Ductile Hero

Steel reinforcing bars (or “rebar”) are the polar opposite. Steel has fantastic tensile strength. You can pull on it with immense force, and it will stretch and stretch before eventually failing. This property is called ductility, and it’s incredibly important for safety. A ductile failure gives warning—things will sag, crack, and creak long before they collapse. A brittle failure, like that of unreinforced concrete, is sudden and without warning.

Steel isn’t as efficient as concrete at handling compression over large areas (it can buckle), but for resisting tension, it’s the undisputed champion.

Reinforced Concrete: A Match Made in Engineering Heaven

Now, let’s embed steel bars into our concrete beam, placing them near the bottom where the tension will be.

When the beam bends:

1. The top of the beam goes into compression. The concrete happily handles this load.
2. The bottom of the beam tries to go into tension. Before the concrete can crack, the steel bars—which are bonded tightly to the concrete—engage and take on the entire tensile force.
3. The steel stretches slightly, but its immense strength prevents the beam from failing.

This is the genius of reinforced concrete. We use two materials together, assigning each one the specific job it was born to do. Concrete handles the compression, and steel handles the tension. This partnership creates a composite material that is strong, durable, economical, and incredibly versatile. Our job as designers is to calculate the precise amount of steel needed to create a perfect, balanced partnership.

Chapter 2: Decoding the Engineer’s Lexicon: Key Terms You Must Know

To perform the calculations, you first need to speak the language. Here are the essential terms we’ll be using throughout this guide.

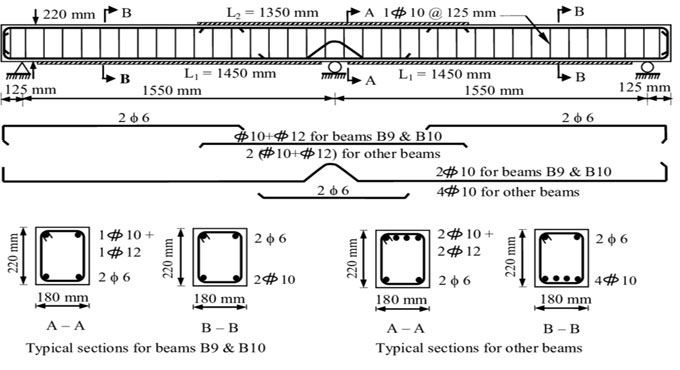
[Image: A simple cross-section of a reinforced concrete beam, clearly labeling width (b), total height (h), effective depth (d), longitudinal rebar (As), stirrups, and concrete cover.]

• Loads: The forces a beam must resist.
  • Dead Loads (D): Permanent forces. This includes the self-weight of the beam, the slab on top of it, flooring, walls, ceilings, and permanent equipment. They are static and unchanging.
  • Live Loads (L): Temporary or transient forces. This includes people, furniture, snow, vehicles, and anything that can move or change over time.
• Internal Forces: The stresses that develop inside the beam in response to the loads.
  • Bending Moment (M): The force that causes a beam to bend (like our “smiling” beam example). It is highest at the mid-span of a simple beam and is responsible for the primary tension and compression. This is what the main longitudinal bars are designed to resist.
  • Shear Force (V): The force that causes one part of the beam to try and slide vertically past the adjacent part. It is highest near the supports. Imagine trying to snap a carrot—the force your hands apply is shear. This is what the smaller, looped bars (stirrups) are designed to resist.
• Material Properties:
  • Compressive Strength of Concrete (f’c): The maximum compressive stress concrete can withstand before crushing. It’s measured in psi (pounds per square inch) or MPa (Megapascals). A common value for residential/commercial construction is 3,000 psi or 4,000 psi (around 25-30 MPa).
  • Yield Strength of Steel (fy): The stress at which steel begins to stretch (yield) permanently. For design, this is considered the “usable” strength of the rebar. A universal standard is Grade 60 rebar, which has an fy of 60,000 psi (or 420 MPa).
• Geometric Properties:
  • Width (b): The horizontal dimension of the beam.
  • Total Height (h): The full vertical dimension of the beam.
  • Effective Depth (d): This is one of the most critical dimensions. It is the distance from the very top of the beam (the compression face) to the center of the main tensile steel. It is not the total height. d = h – concrete cover – stirrup diameter – (main bar diameter / 2).
  • Concrete Cover: A protective layer of concrete over the rebar. Its purpose is to shield the steel from corrosion (rust) and to protect it from fire. The required cover depends on the exposure conditions (e.g., indoor, outdoor, in the ground).
• Reinforcement:
  • Longitudinal Reinforcement (As): The main, large-diameter bars that run along the length of the beam to resist the bending moment. As stands for “Area of steel.”
  • Shear Reinforcement (Stirrups or Links): The smaller, looped bars that are placed vertically at intervals along the beam. They act like stitches, holding the beam together against diagonal shear cracks.

Chapter 3: The Rulebook: Understanding Design Codes and Philosophies

We can’t just design beams based on raw physics. We need a standardized set of rules that ensures safety, reliability, and a consistent approach across the industry. These rules are known as building codes or design codes.

The two most prominent codes for concrete design in the world are:

• ACI 318: Published by the American Concrete Institute, it is the standard in the United States and many other parts of the world.
• Eurocode 2 (EN 1992): The standard used across the European Union and many other countries.

While the specific formulas differ slightly, they are both built upon the same modern design philosophy: Limit State Design (LSD), known in the US as Load and Resistance Factor Design (LRFD).

The core principle is brilliantly simple and safe:

Factored Resistance ≥ Factored Loads

Let’s break that down.

1. We “Factor Up” the Loads: We don’t design for the expected dead and live loads. We multiply them by safety factors greater than 1.0 to account for uncertainty. What if a “100-year storm” happens? What if a room is unexpectedly crowded? The code mandates combinations like 1.2 * Dead Load + 1.6 * Live Load. We intentionally overestimate the forces the beam will ever see.
2. We “Factor Down” the Resistance: We don’t assume the materials are perfectly strong. We multiply the theoretical strength of the concrete and steel by strength reduction factors (φ), which are less than 1.0. This accounts for potential variations in material quality, construction imperfections, and the importance of the structural element. For example, the φ factor for bending is typically 0.90, while for shear it’s 0.75 (reflecting that shear failure is more brittle and dangerous).

This double-layered safety net is the heart of modern structural design. We design for an overestimated load and an underestimated strength. The resulting structure has a very high, but not infinite, margin of safety.

For our worked example, we will be using the principles and formulas derived from ACI 318.

Chapter 4: The Main Event: Step-by-Step Flexural Design (Singly Reinforced Beam)

This is where theory becomes reality. We are going to design the main longitudinal reinforcement for a standard, simply supported concrete beam.

The Problem Statement

Let’s imagine we need to design a rectangular beam inside a commercial building. Here is our given information:

• Function: The beam supports a floor slab.
• Span Length (L): 24 feet
• Loads:
  • Dead Load (D): 1.1 kips/ft (this includes the beam’s own weight)
  • Live Load (L): 1.5 kips/ft
• Material Properties:
  • Concrete Strength (f’c): 4,000 psi
  • Steel Yield Strength (fy): 60,000 psi (Grade 60)
• Beam Dimensions (Initial Guess):
  • Width (b): 14 inches
  • Height (h): 24 inches

Our goal is to determine the required Area of Steel (As) and select the appropriate number and size of rebar.

Step 1: Calculate the Factored Load (Wu) and Factored Moment (Mu)

First, we apply our safety factors to the loads to find the “ultimate” or factored load, Wu.

• ACI Load Combination: Wu = 1.2 * D + 1.6 * L
• Wu = 1.2 * (1.1 kips/ft) + 1.6 * (1.5 kips/ft)
• Wu = 1.32 + 2.40 = 3.72 kips/ft

Now, we calculate the maximum bending moment this load will create. For a simply supported beam with a uniformly distributed load, the maximum moment occurs at the center of the span and is given by the classic formula:

• Maximum Moment Formula: Mu = (Wu * L^2) / 8
• Mu = (3.72 kips/ft * (24 ft)^2) / 8
• Mu = (3.72 * 576) / 8 = 267.84 kip-ft

To make our units consistent for the next steps, let’s convert this to kip-inches:

• Mu = 267.84 kip-ft * 12 in/ft = 3214.1 kip-in

This Mu is the moment the beam must be strong enough to resist.

Step 2: Determine Geometric and Material Properties

We need to calculate our effective depth d and a material constant β1.

• Calculate Effective Depth (d):
  Let’s assume standard conditions:
  • Concrete Cover = 1.5 inches
  • Stirrup Diameter = #3 bar (0.375 inches)
  • Main Bar Size (Guess) = #8 bar (1.0 inch diameter)
    d = h – cover – stirrup_dia – (main_bar_dia / 2)
    d = 24″ – 1.5″ – 0.375″ – (1.0″ / 2) = 21.625 inches
• Calculate Beta_1 (β1):
  β1 is a factor that relates the depth of the rectangular stress block in concrete to the depth of the neutral axis. According to ACI 318:
  • For f’c ≤ 4,000 psi, β1 = 0.85.
  • Since our f’c is 4,000 psi, we use β1 = 0.85.

Step 3: Calculate the Required Reinforcement Ratio (ρ)

The reinforcement ratio, ρ (rho), is the ratio of the steel area to the concrete area (As / (b*d)). It’s the key variable that tells us what percentage of the beam’s cross-section should be steel.

This step involves solving a quadratic equation derived from the internal forces of the beam. A common and direct formula used by engineers is:

ρ = (0.85 * f’c / fy) * [1 – sqrt(1 – (2 * Rn) / (0.85 * f’c))]

First, we need to calculate Rn, which is a term related to the required moment strength.

• Rn = Mu / (φ * b * d^2)
  • φ (Strength Reduction Factor for Bending) = 0.90
  • Mu = 3214.1 kip-in
  • b = 14 in
  • d = 21.625 in
• Rn = 3214.1 / (0.90 * 14 * (21.625)^2)
• Rn = 3214.1 / (5882) = 0.5464 ksi (or 546.4 psi)

Now plug Rn back into the formula for ρ:

• Let’s convert f’c to ksi for consistency: 4,000 psi = 4 ksi. And fy = 60 ksi.
• ρ = (0.85 * 4 / 60) * [1 – sqrt(1 – (2 * 0.5464) / (0.85 * 4))]
• ρ = (0.0567) * [1 – sqrt(1 – 1.0928 / 3.4)]
• ρ = (0.0567) * [1 – sqrt(1 – 0.3214)]
• ρ = (0.0567) * [1 – sqrt(0.6786)]
• ρ = (0.0567) * [1 – 0.8238]
• ρ = (0.0567) * [0.1762]
• ρ = 0.0100

This is our target steel ratio.

Step 4: Check Minimum and Maximum Steel Requirements

The code provides limits on how much steel we can use.

• Minimum Steel (As,min): This is to prevent an overly brittle failure if the concrete cracks. A minimum amount of rebar ensures the steel can pick up the load.
  • As,min is the larger of (3 * sqrt(f’c) / fy) * b * d and (200 / fy) * b * d.
  • As,min = (3 * sqrt(4000) / 60000) * 14 * 21.625 = 0.957 in^2
  • As,min = (200 / 60000) * 14 * 21.625 = 1.009 in^2 <– This one governs.
• Maximum Steel (ρ_max): This is the most critical check. It ensures the beam will fail in a ductile, tension-controlled manner (steel yields before concrete crushes). ACI 318 achieves this by requiring the strain in the steel (εt) to be at least 0.005.
  • The corresponding maximum reinforcement ratio for εt = 0.005 is:
  • ρ_max = (0.85 * β1 * f’c / fy) * (εu / (εu + 0.005)) where εu (ultimate strain of concrete) is 0.003.
  • ρ_max = (0.85 * 0.85 * 4 / 60) * (0.003 / (0.003 + 0.005))
  • ρ_max = (0.04817) * (0.003 / 0.008) = 0.01806

Now, let’s check our calculated ρ:

• ρ = 0.0100
• Is ρ < ρ_max (0.01806)? Yes.
• Is ρ > ρ_min (which corresponds to As,min = 1.009 in^2)? We will check this in the next step.

Our design is valid and will lead to a safe, ductile beam.

Step 5: Calculate Required Steel Area (As)

Now we convert our ratio back into a physical area of steel.

• As = ρ * b * d
• As = 0.0100 * 14 in * 21.625 in
• As,required = 3.028 in^2

Let’s check this against our minimum: As,required (3.028 in^2) is greater than As,min (1.009 in^2). So we are good.

Step 6: Select the Rebar

Our final task is to choose a combination of standard rebar sizes that provides at least 3.028 in² of steel area.

• Common Rebar Areas:
  • #7 bar: 0.60 in²
  • #8 bar: 0.79 in²
  • #9 bar: 1.00 in²
  • #10 bar: 1.27 in²

Let’s try some combinations:

• Three #9 bars: 3 * 1.00 = 3.00 in² (Slightly too low)
• Four #8 bars: 4 * 0.79 = 3.16 in² (Looks good)
• Three #10 bars: 3 * 1.27 = 3.81 in² (A bit oversized, but also works)

Let’s choose 4 #8 bars. The provided area As,provided = 3.16 in² is greater than the required As,required = 3.028 in².

Step 7: Final Check of Beam Width and Spacing

We must ensure our chosen bars physically fit inside the 14-inch wide beam with adequate spacing for concrete to flow between them.

• Required width = (2 * cover) + (2 * stirrup_dia) + (4 * bar_dia) + (3 * spacing)
• Let’s assume a minimum spacing of 1 inch (or the bar diameter, whichever is larger).
• Required width = (2 * 1.5″) + (2 * 0.375″) + (4 * 1.0″) + (3 * 1.0″)
• Required width = 3″ + 0.75″ + 4″ + 3″ = 10.75 inches

Our beam width b = 14 inches is greater than the required 10.75 inches. The bars fit perfectly.

Flexural Design is Complete! We will use a 14″x24″ beam with 4 #8 longitudinal bars at the bottom.

Chapter 5: Handling the Shear Force – Designing the Stirrups

We’re not done yet. We’ve designed for bending, but we also have to resist the shear force, which is highest near the supports.

Step 1: Calculate the Factored Shear Force (Vu)

The maximum shear for a simply supported beam is at the face of the support.

• Vu,max = Wu * L / 2
• Vu,max = 3.72 kips/ft * 24 ft / 2 = 44.64 kips

However, the code allows us to calculate the design shear at a distance d from the face of the support, as any cracks will form diagonally away from the support.

• Vu @ d = Vu,max – Wu * d
• Vu @ d = 44.64 kips – 3.72 kips/ft * (21.625 in / 12 in/ft)
• Vu @ d = 44.64 – 6.71 = 37.93 kips

This is our design shear force.

Step 2: Calculate the Shear Capacity of the Concrete (Vc)

The concrete itself can resist some shear. A simplified ACI formula is:

• Vc = 2 * sqrt(f’c) * b * d
• Vc = 2 * sqrt(4000) * 14 * 21.625
• Vc = 2 * 63.25 * 302.75 = 38,300 lbs = 38.3 kips

Step 3: Determine if Stirrups are Needed

The code requires stirrups if Vu is greater than half the concrete’s capacity (0.5 * φ * Vc).

• φVc = 0.75 * 38.3 kips = 28.73 kips
• 0.5 * φVc = 14.36 kips

Our design shear Vu = 37.93 kips. Since 37.93 kips > 14.36 kips, stirrups are required.

Step 4: Calculate Required Shear from Stirrups (Vs)

The stirrups must resist the shear force that the concrete cannot.

• Vs,required = (Vu – φVc) / φ
• Vs,required = (37.93 – 28.73) / 0.75 = 12.27 kips

Step 5: Calculate Required Stirrup Spacing (s)

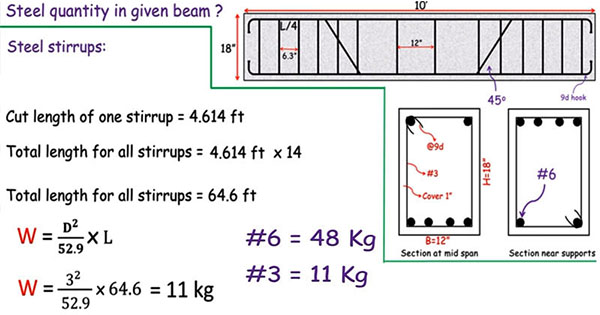
Now we find how far apart our stirrups need to be. Let’s use #3 U-shaped stirrups. The area Av for a U-stirrup has two “legs” crossing the potential crack.

• Area of a #3 bar = 0.11 in²
• Av = 2 * 0.11 in² = 0.22 in²

The formula for spacing is:

• s = (Av * fy * d) / Vs
• s = (0.22 in² * 60 ksi * 21.625 in) / 12.27 kips
• s = 23.2 inches

Step 6: Check Maximum Spacing Requirements

The calculated spacing is not the final answer. The code imposes strict maximum limits to ensure a crack can’t form between stirrups.

• Max spacing is the lesser of d/2 and 24 inches.
• d/2 = 21.625 / 2 = 10.81 inches
• 24 inches

The maximum allowable spacing is 10.81 inches. Let’s round down to a practical number: 10 inches.

Since 10 inches is much less than our calculated required spacing of 23.2 inches, the maximum spacing limit governs our design.

Shear Design is Complete! We will use #3 U-stirrups spaced at 10 inches on center along the length of the beam. (Note: In practice, spacing is often tighter near supports and wider at the mid-span where shear is lower).

Chapter 6: Beyond the Basics – Advanced Topics

Our example covered a fundamental “singly reinforced” rectangular beam. The world of concrete design is much larger. Here are a few key concepts to be aware of:

• Doubly Reinforced Beams: What if an architect says our beam can only be 18 inches tall instead of 24? The reduced depth might not provide enough of a “lever arm” for the concrete to handle the compression. In this case, we add steel in the compression zone (at the top of the beam) to help the concrete. This is a doubly reinforced beam.
• T-Beams: In most buildings, beams are cast monolithically with the floor slab. This means the beam can “borrow” a portion of the slab on either side to help resist compression. This creates a much wider and more efficient T-shaped compression zone, making the beam significantly stronger in bending.
• Serviceability (Deflection and Cracking): Our entire calculation was based on “ultimate strength”—preventing collapse. But a beam that is safe but sags so much that floors are sloped and walls crack is not a successful design. Engineers must also perform serviceability checks to calculate the expected long-term deflection and ensure crack widths are kept to a visually acceptable minimum.

Chapter 7: Common Pitfalls and Pro Tips

• Mistake 1: Confusing h and d. All flexural calculations use the effective depth d, not the total height h. This is a classic student error.
• Mistake 2: Unit Conversion Errors. Mixing kips, pounds, inches, and feet in the same equation is a recipe for disaster. Be meticulously consistent.
• Mistake 3: Ignoring Minimum/Maximum Steel. Forgetting to check As,min and ρ_max can lead to a design that doesn’t meet code requirements for safety and ductility.
• Pro Tip 1: Sketch Everything. Draw a cross-section of your beam. Draw the loading diagram. Visualizing the problem helps prevent simple errors.
• Pro Tip 2: Understand the “Why.” Don’t just plug numbers into formulas. Understand why the reduction factor for shear is lower than for flexure. Understand why there is a maximum steel limit. This deeper knowledge separates a technician from an engineer.

Chapter 8: The Digital Engineer: Software in Beam Design

No modern engineering firm designs beams entirely by hand like our example. Software is an indispensable tool.

• Full Analysis Suites (ETABS, SAP2000, STAAD.Pro): These powerful programs model entire buildings. They calculate the moments, shears, and axial loads on every beam, column, and wall automatically. They can also perform the reinforcement design based on your chosen code.
• Component Design Software: Simpler tools that focus on designing a single element, like a beam or a column.
• Spreadsheets: Many engineers build their own custom spreadsheets (like the one we just walked through) to have full control and transparency over the calculations.

However, a fundamental principle applies to all software: Garbage In, Garbage Out. The software is only as good as the engineer using it. If you don’t understand the principles from our manual calculation, you will not be able to properly input the data, interpret the results, or spot an error when the software produces a nonsensical answer.

Conclusion: Building with Confidence

We’ve journeyed from the basic concept of a concrete-steel partnership to a detailed, code-compliant design of a structural beam. We’ve seen that every single reinforcing bar is placed with purpose, dictated by the laws of physics and the rigorous demands of safety codes.

The calculations are a process of:

1. Determining the forces the beam will face.
2. Applying safety factors to both loads and materials.
3. Calculating the precise amount of steel needed to handle tension (flexure).
4. Verifying that the design will be ductile and safe.
5. Adding steel “stitches” (stirrups) to handle diagonal shear forces.

This intricate dance between concrete and steel, guided by calculation, is what allows us to build soaring skyscrapers, vast bridges, and safe, comfortable homes. The strength is unseen, but it is not unintentional. It is engineered.

Disclaimer: This article is for educational and informational purposes only. The design of structural elements carries significant risk and should only be performed by a licensed professional engineer in accordance with the governing building codes for your jurisdiction. Do not use this guide for the design or construction of any real-world project.